In graduate school I took several courses on Computational Fluid Dynamics (CFD). During one of these courses, a classmate and I worked together to model a driven cavity flow. Driven cavity flows appear quite often in our regular lives. For example, driven cavity flows are often encountered in transportation such as a convertible car, or when an airplane is about to deploy the landing gear. In 2-D, a driven cavity flow can be simplified as the following:
To solve this flow problem numerically, we assumed steady state flow, no body forces, no source terms, and constant fluid properties. The mass and momentum equations governing the flow are the following:
To discretize the domain, we used a staggered grid configuration and the equations were solved iteratively using the Semi-Implicit Method for Pressure Linked Equations (SIMPLE algorithm) with Upwind Differencing Scheme (UDS).
Visually, the velocity boundary conditions can be represented as follows:
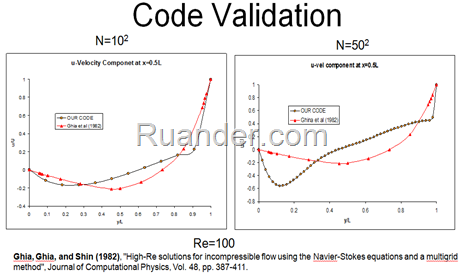
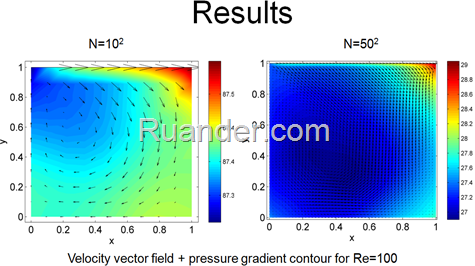
We found that it was quite difficult and computationally expensive to converge a solution. Small relaxation factors seemed to aid in the convergence process. Nevertheless, we sucessfully converged a solution with the relatively low Re=100 with 2 different grid sized.
This is an example of the residuals as a function of iteration number:
In case someone is interested, here is the MATLAB code we wrote (all rights reserved):
clear
clc
close all
%% Constants
rho=1; % kg/m^3
mu=1e-5; % N/m-s
% Geometery
M=10; % Square Grid Size
N=M;
dx=.001/N; % meters, square cavity with side of 1
dy=dx; % meters
% Convergence
alpha_p=.001; % Pressure under-relaxtion
alpha_u=.02; % u-momentum under-relaxation
alpha_v=.02; % v-momentum under-relaxation
max_iter=200000; % maximum number of iterations
max_res=1e-6; % Maximum Residual
inner_iter=1; % Number of iterations before velocity is updated
% Parameters
Dn=mu*dx/dy;Ds=Dn;
De=mu*dy/dx;Dw=De;
% Boundary Conditions
P_free=10; % Pascals
u_free=1; % meters/second
Re=rho*.001*u_free/mu;
%% Creating the variables (initial guesses)
% Starred velocities
u_s=zeros(M+2,N+1); % m/s
u_s(1,:)=u_free*ones(1,N+1);
u_s(2:end-1,2:end-1)=u_free*ones(size(u_s)-2);
u_s=(rot90(u_s,3)); % rotating to get i corresponding
% to an x column and j to a y row
v_s=zeros(M+1,N+2); % m/s
v_s(2:end-1,2:end-1)=u_free*ones(size(v_s)-2);
v_s=(rot90(v_s,3)); % rotating to get i corresponding
% %% Load Previous Velocity Solution
% load('10_square_sol.mat','v')
% XI=linspace(0,11,M+1);
% YI=linspace(0,12,N+2);
% [XI YI]=meshgrid(XI,YI);
% X=1:11;
% Y=1:12;
% [X Y]=meshgrid(X,Y);
% v_s = interp2(X,Y,v,XI,YI);
% clear v
% %% Load Previous Pressure Solution
% load('10_square_sol.mat','u')
% XI=linspace(0,12,M+2);
% YI=linspace(0,11,N+1);
% [XI YI]=meshgrid(XI,YI);
% X=1:12;
% Y=1:11;
% [X Y]=meshgrid(X,Y);
% u_s = interp2(X,Y,u,XI,YI);
% clear u
% to an x column and j to a y row
% Old Velocities
u_o=1*u_s; % m/s
v_o=1*v_s; % m/s
% New Velocities
u=u_s; % m/s
apm_u=zeros(size(u)); % The u momentum :a" coefficient matrix
v=v_s; % m/s
apm_v=zeros(size(v)); % The v momentum "a" coefficient matrix
% Acutal Pressure
x=linspace(0,1,M);
y=x;
[x y]=meshgrid(x,y);
z=1./((x-1).^2+(y).^2+.5);
P=P_free*z; % Pascals
P=(rot90(P,3)); % Pascals, rotating to get i corresponding
% to an x column and j to a y row
% Starred Pressure
% %% Load Previous Pressure Solution
% load('10_square_sol.mat','P')
% XI=linspace(0,10,N);
% YI=linspace(0,10,M);
% [XI YI]=meshgrid(XI,YI);
% X=1:10;
% Y=X;
% [X Y]=meshgrid(X,Y);
% P = interp2(X,Y,P,XI,YI);
P_s=P; % Pascals
% Old Pressure
P_o=P; % Pascals
% Pressure Correction
P_p=zeros(size(P)); % Pascals
%% Initiating the Simple Algorithm Infinite Loop
% Begin the while loop
count=0;
residual=zeros(3,max_iter);
while 1
count=count+1; % Counting the iterations
disp(count)
for k=1:inner_iter
%% Solving starred momentum equations
% u=u+.5*exp(-0.05*count);
% v=v+5*exp(-0.1*count);
% P=P+50*exp(-count);
% u-momentum
for i=2:size(u,1)-1
for j=2:size(u,2)-1
% Computing the face fluxes:
Fe=rho*dy/2*(u_o(i+1,j)+u_o(i,j)); Fw=rho*dy/2*(u_o(i,j)+u_o(i-1,j));
Fn=rho*dx/2*(v_o(i,j)+v_o(i+1,j)); Fs=rho*dx/2*(v_o(i,j-1)+v_o(i+1,j-1));
% Computing the "a" coefficients:
ae=De-min(0,Fe); aw=Dw+max(0,Fw);
an=Dn-min(0,Fn); as=Ds+max(0,Fs);
apm_u(i,j)=ae+aw+an+as+(Fe-Fw+Fn-Fs);
u_s(i,j)=1/apm_u(i,j)*(ae*u_s(i+1,j)+aw*u_s(i-1,j)... % x-direction
+an*u_s(i,j+1)+as*u_s(i,j-1)...% y-direction
-dy*(P_s(i,j-1)-P_s(i-1,j-1))); % Pressure term
end % the j loop
end % the i loop
% v-momentum
for i=2:size(v,1)-1
for j=2:size(v,2)-1
% Computing the face fluxes:
Fe=rho*dy/2*(u_o(i,j+1)+u_o(i,j)); Fw=rho*dy/2*(u_o(i-1,j+1)+u_o(i-1,j));
Fn=rho*dx/2*(v_o(i,j+1)+v_o(i,j)); Fs=rho*dx/2*(v_o(i,j)+v_o(i,j-1));
% Computing the "a" coefficients:
ae=De-min(0,Fe); aw=Dw+max(0,Fw);
an=Dn-min(0,Fn); as=Ds+max(0,Fs);
apm_v(i,j)=ae+aw+an+as+(Fe-Fw+Fn-Fs);
v_s(i,j)=1/apm_v(i,j)*(ae*v_s(i+1,j)+aw*v_s(i-1,j)... % x-direction
+an*v_s(i,j+1)+as*v_s(i,j-1)...% y-direction
-dx*(P_s(i-1,j)-P_s(i-1,j-1))); % Pressure term
end % the j loop
end % the I loop
%% Enforcing conservation of mass on the top boundary
% v_s(2:end-1,end)=v_s(2:end-1,end-1);
% for i=2:N+1
% u_s(i,M+2)=u_s(i-1,M+2)+v_s(i,M+1);
% end
%% Solving the pressure correction equations
% Pressure correction loop
for I=1:N
for J=1:M
if I==1 && J==1
% Bottom left corner
ae=rho*dy^2/apm_u(I+1,J+1); aw=0;
an=rho*dx^2/apm_v(I+1,J+1); as=0;
ap=ae+aw+an+as;
b=rho*(dy*u_s(I,J+1)-dy*u_s(I+1,J+1)+dx*v_s(I+1,J)-dx*v_s(I+1,J+1));
P_p(I,J)=1/ap*(ae*P_p(I+1,J)+an*P_p(I,J+1)+b);
elseif I==1 && J~=1 && J~=M
% Left wall
ae=rho*dy^2/apm_u(I+1,J+1); aw=0;
an=rho*dx^2/apm_v(I+1,J+1); as=rho*dx^2/apm_v(I+1,J);
ap=ae+aw+an+as;
b=rho*(dy*u_s(I,J+1)-dy*u_s(I+1,J+1)+dx*v_s(I+1,J)-dx*v_s(I+1,J+1));
P_p(I,J)=1/ap*(ae*P_p(I+1,J)+an*P_p(I,J+1)+as*P_p(I,J-1)+b);
elseif J==1 && I~=1 && I~=N
% Bottom wall
ae=rho*dy^2/apm_u(I+1,J+1); aw=rho*dy^2/apm_u(I,J+1);
an=rho*dx^2/apm_v(I+1,J+1); as=0;
ap=ae+aw+an+as;
b=rho*(dy*u_s(I,J+1)-dy*u_s(I+1,J+1)+dx*v_s(I+1,J)-dx*v_s(I+1,J+1));
P_p(I,J)=1/ap*(ae*P_p(I+1,J)+aw*P_p(I-1,J)+an*P_p(I,J+1)+b);
elseif I==N && J==1
% Bottom right corner
ae=0; aw=rho*dy^2/apm_u(I,J+1);
an=rho*dx^2/apm_v(I+1,J+1); as=0;
ap=ae+aw+an+as;
b=rho*(dy*u_s(I,J+1)-dy*u_s(I+1,J+1)+dx*v_s(I+1,J)-dx*v_s(I+1,J+1));
P_p(I,J)=1/ap*(aw*P_p(I-1,J)+an*P_p(I,J+1)+b);
elseif I==N && J~=1 && J~=M
% Right wall
ae=0; aw=rho*dy^2/apm_u(I,J+1);
an=rho*dx^2/apm_v(I+1,J+1); as=rho*dx^2/apm_v(I+1,J);
ap=ae+aw+an+as;
b=rho*(dy*u_s(I,J+1)-dy*u_s(I+1,J+1)+dx*v_s(I+1,J)-dx*v_s(I+1,J+1));
P_p(I,J)=1/ap*(aw*P_p(I-1,J)+an*P_p(I,J+1)+as*P_p(I,J-1)+b);
elseif I==1 && J==M
% Top Left
ae=rho*dy^2/apm_u(I+1,J+1); aw=0;
an=0; as=rho*dx^2/apm_v(I+1,J);
ap=ae+aw+an+as;
b=rho*(dy*u_s(I,J+1)-dy*u_s(I+1,J+1)+dx*v_s(I+1,J)-dx*v_s(I+1,J+1));
P_p(I,J)=1/ap*(ae*P_p(I+1,J)+as*P_p(I,J-1)+b);
elseif I==N && J==M
% Top Right
ae=0; aw=rho*dy^2/apm_u(I,J+1);
an=0; as=rho*dx^2/apm_v(I+1,J);
ap=ae+aw+an+as;
b=rho*(dy*u_s(I,J+1)-dy*u_s(I+1,J+1)+dx*v_s(I+1,J)-dx*v_s(I+1,J+1));
P_p(I,J)=1/ap*(aw*P_p(I-1,J)+as*P_p(I,J-1)+b);
elseif I~=N && I~=1 && J==M
% Top Row
ae=rho*dy^2/apm_u(I+1,J+1); aw=rho*dy^2/apm_u(I,J+1);
an=0; as=rho*dx^2/apm_v(I+1,J);
ap=ae+aw+an+as;
b=rho*(dy*u_s(I,J+1)+dx*v_s(I+1,J)-dx*v_s(I+1,J+1));
P_p(I,J)=1/ap*(ae*P_p(I+1,J)+aw*P_p(I-1,J)+as*P_p(I,J-1)+b);
else
% Interior nodes
ae=rho*dy^2/apm_u(I+1,J+1); aw=rho*dy^2/apm_u(I,J+1);
an=rho*dx^2/apm_v(I+1,J+1); as=rho*dx^2/apm_v(I+1,J);
ap=ae+aw+an+as;
b=rho*(dy*u_s(I,J+1)-dy*u_s(I+1,J+1)+dx*v_s(I+1,J)-dx*v_s(I+1,J+1));
P_p(I,J)=1/ap*(ae*P_p(I+1,J)+aw*P_p(I-1,J)+an*P_p(I,J+1)+as*P_p(I,J-1)+b);
end % the conditional boundary node statement
end % the J loop
end % the I loop
%% Correcting the pressure and velocities
P=P_s+alpha_p*P_p; % Relaxed Pressure
% u-correction
for i=2:size(u,1)-1
for j=2:size(u,2)-1
u(i,j)=u_s(i,j)+dy/apm_u(i,j)*(P_p(i-1,j-1)-P_p(i,j-1));
end
end
% v-correction
for i=2:size(v,1)-1
for j=2:size(v,2)-1
v(i,j)=v_s(i,j)+dx/apm_v(i,j)*(P_p(i-1,j-1)-P_p(i-1,j));
end
end
%% Enforcing conservation of mass on the top boundary
% v(2:end-1,end)=v(2:end-1,end-1);
%% Relaxing the velocities
% Similar equations to "solving the starred momentum", only the starred
% quantities are the new guesses (both velocity and pressure)
% u-momentum
for i=2:size(u,1)-1
for j=2:size(u,2)-1
% Computing the face fluxes:
Fe=rho*dy/2*(u_o(i+1,j)+u_o(i,j)); Fw=rho*dy/2*(u_o(i,j)+u_o(i-1,j));
Fn=rho*dx/2*(v_o(i,j)+v_o(i+1,j)); Fs=rho*dx/2*(v_o(i,j-1)+v_o(i+1,j-1));
% Computing the "a" coefficients:
ae=De-min(0,Fe); aw=Dw+max(0,Fw);
an=Dn-min(0,Fn); as=Ds+max(0,Fs);
ap=ae+aw+an+as+(Fe-Fw+Fn-Fs);
u(i,j)=alpha_u/ap*(ae*u(i+1,j)+aw*u(i-1,j)... % x-direction
+an*u(i,j+1)+as*u(i,j-1)...% y-direction
-dy*(P(i,j-1)-P(i-1,j-1)))+(1-alpha_u)*u_o(i,j); % Pressure term
end % the j loop
end % the i loop
% v-momentum
for i=2:size(v,1)-1
for j=2:size(v,2)-1
% Computing the face fluxes:
Fe=rho*dy/2*(u_o(i,j+1)+u_o(i,j)); Fw=rho*dy/2*(u_o(i-1,j+1)+u_o(i-1,j));
Fn=rho*dx/2*(v_o(i,j+1)+v_o(i,j)); Fs=rho*dx/2*(v_o(i,j)+v_o(i,j-1));
% Computing the "a" coefficients:
ae=De-min(0,Fe); aw=Dw+max(0,Fw);
an=Dn-min(0,Fn); as=Ds+max(0,Fs);
ap=ae+aw+an+as+(Fe-Fw+Fn-Fs);
v(i,j)=alpha_v/ap*(ae*v(i+1,j)+aw*v(i-1,j)... % x-direction
+an*v(i,j+1)+as*v(i,j-1)...% y-direction
-dx*(P(i-1,j)-P(i-1,j-1)))+(1-alpha_v)*v_o(i,j); % Pressure term
end % the j loop
end % the I loop
%% Enforcing conservation of mass on the top boundary
% v(2:end-1,end)=v(2:end-1,end-1);
% for i=2:N+1
% u(i,M+2)=u(i-1,M+2)+v(i,M+1);
% end
end % the inner iterations
%% Checking for convergence
if sum(isnan(u(:)))+sum(isnan(v(:)))+sum(isnan(P(:)))>=1
disp('Error: Solution has diverged');
break % End the simple algorithm
end
if count>max_iter
disp('Maximum number of iterations has been reached')
break % End the simple algorithm
end
if max(abs(u_o(:)-u(:)))<max_res && max(abs(v_o(:)-v(:)))<max_res && max(abs((P_o(:)-P(:))./P_o(:)))<10*max_res
disp('Success: Solution has converged');
break % End the simple algorithm
else % Plotting the residuals
residual(1,count)=max(abs(u_o(:)-u(:)));
residual(2,count)=max(abs(v_o(:)-v(:)));
residual(3,count)=max(abs((P_o(:)-P(:))./P_o(:)));
figure(1)
plot(1:count,residual(1,1:count),'r-','linewidth',1.5);hold on % u-mom
plot(1:count,residual(2,1:count),'g-','linewidth',1.5); % v-mom
plot(1:count,residual(3,1:count),'b-','linewidth',1.5); % Pressure
plot(1:count,max_res*ones(1,count),'k--','linewidth',1.5);hold off
% legend('u-momentum','v-momentum','Pressure','Maximum
% Residual')
xlabel('Iterations','fontsize',16)
ylabel('Residual','fontsize',16)
set(gca,'fontsize',16,'yscale','log');
set(gcf,'color','white')
drawnow
figure(2)
pcolor(P);shading interp;drawnow
pause(0.01)
end
%% Re-initiating old values
% Since the algorithm did not converge, the new values are now the old
% values
u_s=u;
v_s=v;
P_s=P;
u_o=u;
v_o=v;
P_o=P;
end
%% Plotting Results
x=linspace(0,1,N+1);
y=x;
[x y]=meshgrid(x,y);
figure,quiver(x,y,u(:,2:end)',v(2:end,:)',2,'k');hold on
xlabel('x','fontsize',16);
ylabel('y','fontsize',16);
set(gca,'fontsize',16);
x=linspace(0,1,N);
y=x;
[x y]=meshgrid(x,y);
pcolor(x,y,P');shading interp
pco=get(gca,'children');
set(pco(1),'facealpha',.5);
xlabel('x','fontsize',16);
ylabel('y','fontsize',16);
set(gca,'fontsize',16);
colorbar
% figure,surf(u);shading interp
% figure,surf(v);shading interp






When we consider super cars, we find that there are many different kinds of car. We have Ferrari and Porsche, possibly 2 of the most famous super car. But, the Lamborghini is a cut above the rest. And here is why. Lamborghini Rentals Near Me
ReplyDeleteThe company has a network of trusted and experienced drivers who are skilled in handling exotic cars and ensuring their safe transport. Exotic Car Transport
ReplyDeleteUse Color-Coded Labels for Different Rooms: Enhance organization by assigning a specific color to each room. This helps movers know where each box belongs, including any boxes with auto or luxury car parts or accessories. Cheapest Way to Ship a Motorcycle
ReplyDelete