In a previous post, the laminar plate boundary layer was discussed. However, in many applications the flow is turbulent rather than laminar. For a turbulent boundary layer flow, a universal “law of the wall” has been determined from both experiments and analytically. This universal law takes the following logarithmic profile:
Where u+ and y+ are the non dimensional velocity and cross-stream direction variable and K and C+ are constants. Known as the Karman constant, k has been shown analytically to have a value of 0.41. C+ is an integration constant and it has been shown experimentally to have a value around C+ = 5 for a smooth surface. However, if the surface is rough, the value of C+ will depend on the stream-wise direction, x. It can be shown that for a fully rough surface, the value of C+ has the following dependency with the x-direction Reynolds’s number:
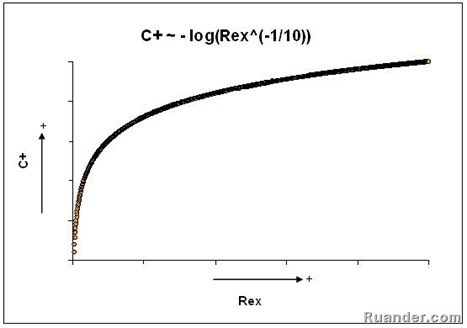
From the figure above, we see then that the value of C+ increases rapidly at first but then it levels off eventually. If one compares the velocity profile for a smooth vs. a fully rough surface along a plate, it can be concluded that the effect roughness on the surface affect the velocity profile more near the leading edge and that as the flow move in the stream direction this affect become less and the rough surface profile approaches the smooth surface profile for large values of x. This effect can be observed in the following graphs one for an x location of 0.3m and the other one for an x location of 12 m.
Where u+ and y+ are the non dimensional velocity and cross-stream direction variable and K and C+ are constants. Known as the Karman constant, k has been shown analytically to have a value of 0.41. C+ is an integration constant and it has been shown experimentally to have a value around C+ = 5 for a smooth surface. However, if the surface is rough, the value of C+ will depend on the stream-wise direction, x. It can be shown that for a fully rough surface, the value of C+ has the following dependency with the x-direction Reynolds’s number:

From the figure above, we see then that the value of C+ increases rapidly at first but then it levels off eventually. If one compares the velocity profile for a smooth vs. a fully rough surface along a plate, it can be concluded that the effect roughness on the surface affect the velocity profile more near the leading edge and that as the flow move in the stream direction this affect become less and the rough surface profile approaches the smooth surface profile for large values of x. This effect can be observed in the following graphs one for an x location of 0.3m and the other one for an x location of 12 m.



No comments:
Post a Comment